Learn how to derive the equations behind mismatch detection assays
We recently wrote a featured article describing assessment of gene editing with DNA mismatch detection assays where we explain the relationship between percent editing and percent cleavage. For many, this is a non-intuitive result, but it is easy to understand after examining the derivation of Eq. 1. The underlying mathematics also reveals several fundamental assumptions not often discussed.
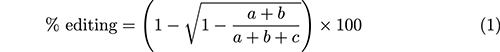
In Eq. 1, a, b, and c represent the density of the three bands in an agarose gel, which result from running a T7EI mismatch detection assay, depicted in Fig. 1c.
Mismatch detection assays
Our previous article describes the T7EI assay in detail, but it can be summarized in three broad steps.
- Step 1: After a gene editing experiment, DNA is collected from the experimental population. Double stranded DNA regions straddling the intended edit site are PCR-amplified. The idea is to amplify wild type (WT) amplicons (if it was not edited) or edited amplicons (if it has an insertion or deletion; Fig. 1a).
- Step 2: The resulting pool of amplicons is then melted and allowed to reanneal before adding T7EI. The strands will reanneal randomly if the sequences are similar between WT and edited (Fig. 1b). We will assume that any reannealed amplicons with a mismatch are cleaved upon the addition of T7EI. However, it is known that mismatch detection enzymes are not 100% efficient at identifying and cutting all types of mismatches or bulges/distortions in DNA.1,2
- Step 3: An agarose gel run on the resulting mixture gives the fraction of reannealed amplicons that were cleaved as the density of the two lower, cut bands (separate from the upper, uncut WT band; Fig. 1c).

The Mathematics
Calculating the fraction of alleles that have an edit from the fraction of amplicons cut by T7EI in the gel (Eq. 1) essentially boils down to calculating the probability that two reannealed strands (from step 2) will have a mismatch. If strands reanneal randomly, we can calculate the probability of each possible reannealing combination (WT-WT, WT-edited, and edited-edited) in terms of the fraction editing, pe (Fig 2). And if we make the simplifying assumption that any mismatch will be cleaved by T7EI, we can calculate the cutting probability for each scenario (Fig. 2).

Once we have defined these probabilities, we can calculate the fraction of reannealed amplicons that we expect to be cleaved (expected fc). This is simply the reannealing probability for a given state i multiplied by the probability that T7EI will cleave state i, summed over all N possible states.
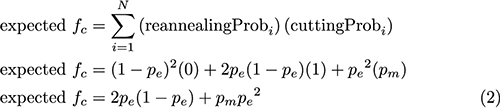
Equating the fraction of reannealed amplicons cleaved in the experiment (fc) to Eq. 2 gives us
![]()
where pe is the editing probability and fc is the following experimentally measured ratio (see Fig. 1c)
![]()
Solving Eq. 3 gives us the general formula for fraction editing in terms of fc.
![]()
Now, all that remains to be done is to calculate (or approximate) pm for a given experiment. We will now outline several ways in which this can be done.
Approximation 1: All Edits Are Unique
If we assume that no two edited strands are identical (i.e. edits are random), reannealed edited-edited strands (from Fig. 2) will always have a mismatch. If there is always a mismatch, we can approximate pm = 1, since T7EI should always cleave the amplicon. Substituting pm = 1 into Eq. 4 gives us
![]()
which is identical to Eq. 1 after multiplying by 100! This is the approximation often taken in literature. As a mathematical side note, there are two solutions given by Eq. 4, but, in this case, we can discard the second, which gives a non-physical result (i.e. pe > 1, which violates the requirement that pe range between 0 and 1).
Key Assumptions
Since this is the approximation most often taken in literature, it is worth noting several key assumptions in the derivation of Eq. 5. These assumptions are likely reasonable in many experiments, but are useful to consider.
- Reannealing is equally likely to occur between any two amplicon strands. If this were not the case, it is difficult to make any conclusions with this assay.
- No two edits are the same. If edits are decidedly non-random, you can no longer assume that edited-edited reannealing will result in T7EI cleavage. See the next two sections for examples (Approximations 2 and 3).
- There are many cells in each gene editing experiment. Were this not the case, we cannot approximate the probabilities as we have in Fig. 2.
There are, of course, other potential concerns common to many assays that we will not discuss in this article: potential PCR amplification bias, gel image saturation, mismatch/deformation bias of the given nuclease (e.g. T7EI versus CEL12).
Approximation 2: All Edits Are Identical
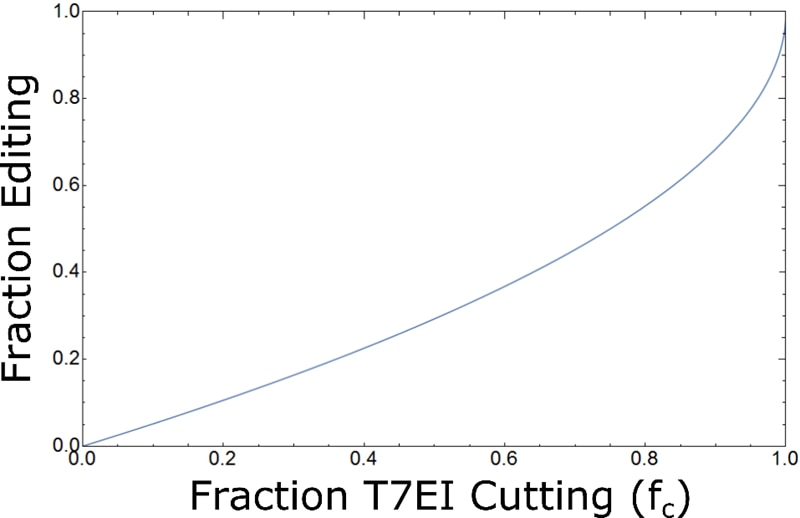
As we saw in the previous section, one key assumption to Eq. 1 is that no two edited strands are identical. What if the opposite were true and all edits were the same? This situation can also arise in the context of genotyping plants (the original application of mismatch detection) when there is a naturally-occurring heterozygous locus.4 In this situation, we can approximate pm = 0 since reannealed edited-edited strands (Fig. 2) are identical and will therefore not be cleaved by T7EI. Substituting pm = 0 into Eq. 4 gives us
![]()
which has two valid solutions. In this situation (as shown in Fig. 4), there is no way to determine from a gel image alone whether an fc of 0 is the result of 0% editing or 100% editing! Also, note that it is no longer possible to measure an fc > 0.5, which makes intuitive sense. Under these assumptions, the maximum possible fc occurs when the probability of a mismatch is maximized [2pe(1-pe) in Fig. 2], which occurs at fc = 0.5.
Approximation 3: N Equally Likely Edits
In the first approximation, we assumed that no two edits were the same, and in the second approximation we took the opposite assumption (all edits are identical), which resulted in two different estimates for the fraction editing (Eqs. 5 and 6). It is reasonable to guess that the truth for any given experiment lies somewhere in between. For this approximation, we take the more general case where there are N distinct edits that are equally likely to occur.
The probability of reannealed edited-edited strands having a mismatch is one minus the probability of edited-edited strands matching (Eq. 7).
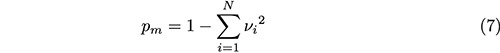
νi is probability of selecting edited strand i from the pool of all N edited strands. In this approximation, νi = 1/N since all N edits are equally likely, which reduces Eq. 7 to

Plugging pm into Eq. 4 gives the fraction editing for N equally likely edits.

Both solutions in Eq. 9 are valid for values of fc that give pe between 0 and 1 (and rational). Notice that limiting values of N in Eq. 9 give the same result as our first two approximations. If all edits are unique, there are an (effectively) infinite number of possible edits (N → ∞), which gives us Eq. 5 (approximation 1). If all edits are identical, there is a single possible edit (N = 1), which reduces to Eq. 6 (approximation 2).

As you can see from Fig. 5, as the number of distinct edits increases beyond N=16, the estimated fraction editing begins to closely approximate the published formula (Eq. 1). Although Eq. 1 is likely a good approximation for most experiments, there is evidence that certain CRISPR editing events will produce highly non-random results with only a few prevalent edits.3 We have also observed this in some experiments (Fig. 6); we treat our estimate of the percent editing as a lower limit and take care to not over-interpret small differences between T7EI assay results.

Summary
When analyzing mismatch detection assays, we often do not know the underlying distribution of editing events (e.g. Fig. 6), which can differ between target site, target sequence, and cell line. This translates to uncertainty in the probability of two edited strands reannealing with a mismatch (pm in Eq. 4). Due to this uncertainty, it is often best to use the standard equation (Eq. 1) when calculating the percent editing, which provides a lower limit. Keeping in mind that this can be a (sometimes substantial) underestimate of the true percentage editing, we take care to not over-interpret minor differences between different mismatch detection assays.
Using these calculations as a starting point, it is straightforward to begin relaxing other assumptions and testing for their consequences. We hope that taking a closer look at the mathematics has helped make mismatch detection assay analysis easier to understand!
T7EI Web Tool
Check out our T7EI Calculator available as part of the bioinformatics group’s beta tools offering (freely available to the public). If you find this tool useful or would like to see additional features added, contact us.
Authors: Matthew R. Perkett, Bioinformatics Developer; Emily M. Anderson, Senior Scientist; Jesse Stombaugh, Bioinformatics Developer
References
- R. D. Mashal, J. Koontz, J. Sklar, Detection of mutations by cleavage of DNA heteroduplexes with bacteriophage resolvases. Nat Genet 9, 177-183 (1995).
- L. Vouillot, A. Thelie, N. Pollet, Comparison of T7EI and surveyor mismatch cleavage assays to detect mutations triggered by engineered nucleases. G3 (Bethesda) 5, 407-415 (2015).
- M. van Overbeek, et. al., DNA Repair Profiling Reveals Nonrandom Outcomes at Cas9-Mediated Breaks. Mol Cell 63(4), 633-646 (2016).
- N Paniego, C. Fusari, V. Lia, A. Puebla, SNP genotyping by heteroduplex analysis. Methods Mol Biol 1245, 141-150 (2015).
Additional Resources
CRISPR Guide RNA
- Lentiviral and synthetic reagents for targeted gene knockout
Edit-R Synthetic Positive crRNA Controls and Detection Primers
- Species-specific crRNAs targeting well-characterized genes, as well as mismatch detection assay primers, to determine the effectiveness of your gene editing conditions for maximal efficiency.
